Klasifikace a systémová analýza - AISPV1001

Tento požadavek se týká určení hranic analyzovaného celku i jeho částí. Každou třídu je třeba jednoznačně definovat v prostoru (rozsahem) a v čase. Hledáme tedy odpovědi na otázky: Které prvky do třídy patří a které ne? V jakém období / při jaké události je prvek součástí třídy? V jakém kontextu třída existuje? Například pro třídu "Čtenář" mohou být k dispozici tato vymezení: Čtenář je ten, kdo umí číst. Čtenář je ten, kdo právě čte. Čtenář je ten, kdo je registrovaným uživatelem knihovny. Čtenář je ten, kdo předčítá text audioknihy. Čtenář je ten, kdo poslouchá text audioknihy. Je zjevné, že každé z vymezení ohraničí jinou množinu objektů.

Tradičním nástrojem jednoznačného vymezení jsou identifikátory a definice, v ontologickém inženýrství plní tuto úlohu axiomy.

Definice je "relativně úplné, závazné a postačující vystižení obsahu pojmu (definiendum) jinými pojmy (definiens)"[1].

Správně vytvořené intenzionální definice podle vzorce „nejbližší rod – specifické rozdíly“ jsou založeny na generické hierarchii.

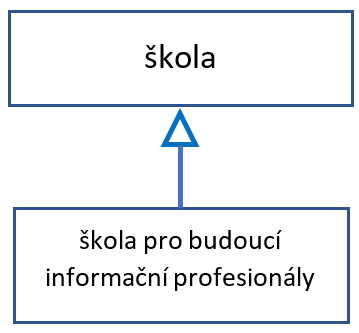
Příklad: ÚISK FF UK Praha je škola pro budoucí informační profesionály. nejbližší rod: škola druhové rozdíly: pro budoucí informační profesionály

Při striktním vymezování členství ve třídě lze na správně definované třídy uplatnit požadavek splnění logické podmínky nutnosti a logické podmínky postačitelnosti. Tyto podmínky řeší otázku, které specifické druhové rozdíly, tj. vlastnosti definovaného objektu, se mají zahrnout do definice.

Podmínka nutnosti znamená: Jestliže je něco prvkem dané třídy, musí to nutně splňovat (všechny) stanovené podmínky. Jinými slovy, podmínka nutnosti definuje množinu vlastností povinných pro každý objekt v extenzi dané třídy. A platí jen tehdy, platí-li současně B. B je tedy nutnou podmínkou pro A. B implikuje A, B => A.

Příklad: Aby bylo možné říci o nějakém objektu, že je to kopretina (A), musí to být květina (B), tj. musí mít všechny vlastnosti, které má květina.

Podmínka postačitelnosti znamená: Jestliže něco splňuje stanovené podmínky, musí to být prvkem dané třídy. B platí jen tehdy, platí-li současně A. Není přitom nutné, aby tuto podmínku splňovaly všechny prvky dané třídy.

Příklad: Stačí, že jsme zjistili, že daný objekt je kopretina (A), tj. že má všechny vlastnosti kopretiny, a můžeme o něm tvrdit, že je to květina (B). Přitom není nutné, aby vlastnosti kopretiny měly všechny ostatní květiny, tj. aby to byla květina, nemusí to být kopretina.

Pokud jsou splněny obě podmínky současně, je vymezení třídy tzv. úplné. A je ekvivalentní B, A<=>B.

Třídy splňující podmínky nutnosti a postačitelnosti jsou někdy označovány jako monotetické, na rozdíl od tříd polytetických, v nichž tyto striktní podmínky nejsou uplatněny.