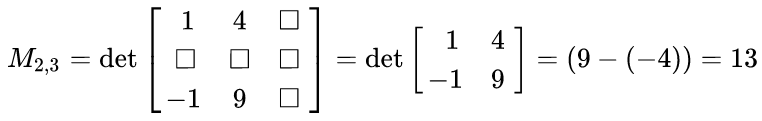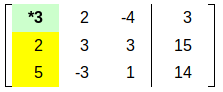Algebra - vocabulary
This dictionary was created by your fellow students mathematicians. It comprises what you should be mostly already familiar with from our winter semester.
Speciální | A | Á | B | C | Č | D | Ď | E | É | Ě | F | G | H | CH | I | Í | J | K | L | M | N | Ň | O | Ó | P | Q | R | Ř | S | Š | T | Ť | U | Ú | Ů | V | W | X | Y | Ý | Z | Ž | VŠE
A |
|---|
annihilatornoun Pronunciation: /ɐnˈaɪ.ə.leɪtə/ Definition: Let M be a left modul over a ring R and let S be a subset of M. The annihilator of S is the set of all r from R such that sr is equal to zero (for all s from S). Source: | |
Associativitynoun Pronunciation: [ə,səʊsɪə'tɪvɪti] Meaning: a property of a binary operation; if it holds, then with more than one of the same operator, the order of operations does not matter Example: if + is an associative operator, then for every three elements a, b, c it holds that a + (b + c) = (a + b) + c Source: | |
B |
|---|
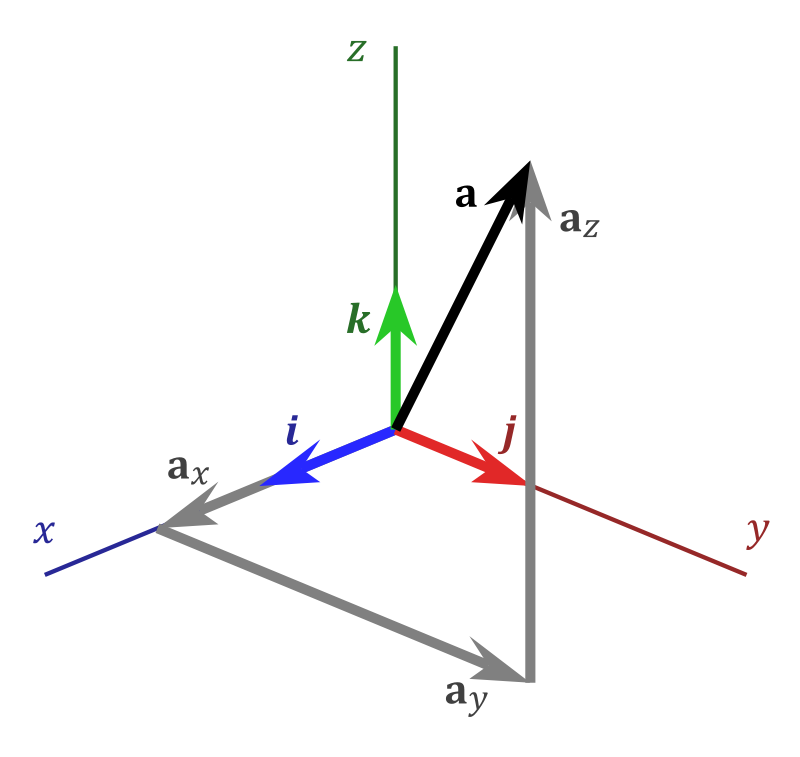
BasisNoun The figure shows the basis vectors i,j, k, and the vector a is a linear combination of them.
| |
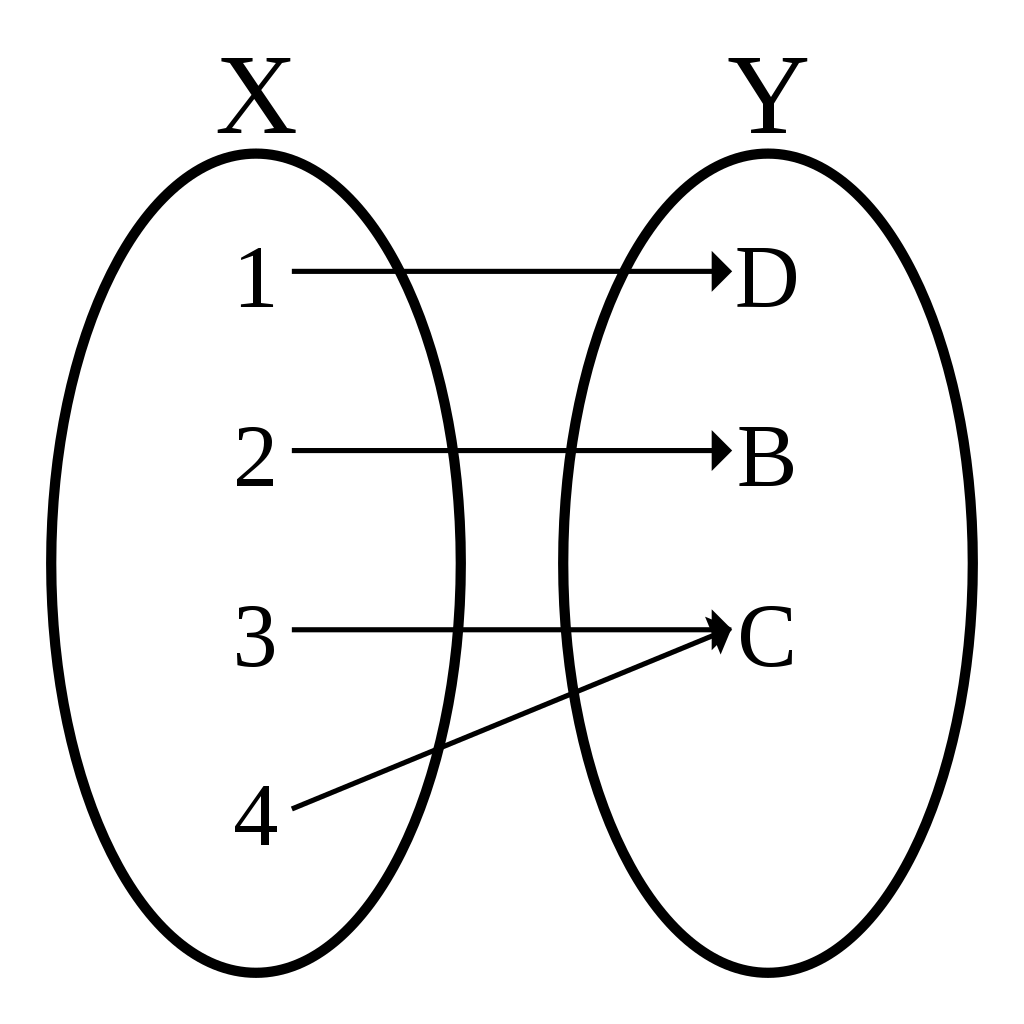
BijectionNoun
| |
C |
|---|
CommutativityNoun Etymology | |
Construction/kənˈstrʌk.ʃən/ A finite sequence of steps. The steps are defined by author of the task, classical example is Eucleidian construction by straightedge and compass. | |
Coprime (integers)Adjective
Antonym Etymology | |
D |
|---|
DeterminantNoun Pronunciation | |
DimensionDimension, n. Pronounciation: /dɪˈmɛnʃən/ Meaning: 1) Geometry. A mode of linear measurement, magnitude, or extension, in a particular direction; usually as co-existing with similar measurements or extensions in other directions. 2) Algebra. Since the product of two, or of three, quantities, each denoting a length (i.e. a magnitude of one dimension), represents an area or a volume (i.e. a magnitude of two, or of three, dimensions), such products themselves are said to be of so many dimensions; and generally, the number of dimensions of a product is the number of the (unknown or variable) quantities contained in it as factors (known or constant quantities being reckoned of no dimensions); any power of a quantity being of the dimensions denoted by its index. Source: | |
Distributivitynoun Pronunciation: [dɪsˌtrɪbjʊˈtɪvɪti] Meaning: a property connecting addition and multiplication; for all numbers a, b, c it holds that a(b+c) = ac + bc and (a+b)c = ac + bc Sources: https://www.oed.com/view/Entry/55790?redirectedFrom=distributivity#eid | |
Dot productnoun Pronunciation: [dɒt 'prɒdʌkt] Meaning: the sum of the products of corresponding coordinates of two real vectors, or of the products of the coordinates of the second of two complex vectors and the complex conjugates of the corresponding coordinates of the first Source: https://www.oed.com/view/Entry/56962?redirectedFrom=dot+product#eid1265788880 | |
E |
|---|
eigenvaluen. Pronunciation ˈīgənˌvalyo͞o Meaning One of those special values of a parameter in an equation for which the equation has a solution. Etymology translating German eigenwert | |
EigenvectorNoun
| |
Embedding (also imbedding)Noun | |
F |
|---|
fieldnoun Pronunciation: /fiːld/ Definition: Field is an algebraic structure defined as 7-tuple of set, binary operations on this set (addition and multiplication), two unary operations (multiplicative inverse) and two nullary operations (0 and 1). With folowing axioms:
source: | |
Field of fractionsnoun pronunciation: [ fēld əv ˈfrakSHəns ] synonyms: fraction field, field of quotients, or quotient field meaning: Field of fractions of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain examples: The field of fractions of the ring of integers is the field of rationals, i.e. Given a field | |
G |
|---|
Gaussian elimination algorithmGaussian, adj. Elimination, n. (created from a verb eliminate, /ᵻˈlɪmᵻneɪt/, and a suffix -ion) Algorithm, n. Pronounciation: /ˈɡaʊsɪən/, /ᵻˌlɪmᵻˈneɪʃn/, /ˈalɡərɪð(ə)m/ Meaning: Gaussian: Discovered or formulated by Gauss. Elimination: The removal of a constant, variable, factor, etc., from a system of equations or a matrix by algebraic manipulation. Algorithm: A procedure or set of rules used in calculation and problem-solving; (in later use spec.) a precisely defined set of mathematical or logical operations for the performance of a particular task. Source: OED | |
Greatest Common Divisor (GCD) domainnoun pronunciation: [ ˈgreytist ˈkämən diˈvīzər dōˈmān ] meaning: is an integral domain with the property that any two elements have a greatest common divisor (GCD) property: If R is a GCD domain, then the polynomial ring R[X1,...,Xn] is also a GCD domain. | |
Group /ɡruːp/a set of operations so constituted that the product of any number of these operations is always itself a member of the set. In later use more generally: a set of elements together with an operation for combining any two of them to form a third element which is also in the set, the operation satisfying certain conditions. Etymology: French groupe, grouppe small detachment of soldiers (1574), arrangement of two or more figures or objects in a design . 1668), (in music) series of notes forming an ornament, run, etc., or linked by a slur (1703), number of things having some related properties or attributes in common (1726) | |
Group homomorphismnoun pronunciation: [ gro͞op ˌhōməˈmôrˌfizəm ] meaning: given two groups, (G, ∗) and (H, ·), a group homomorphism from (G, ∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that where the group operation on the left hand side of the equation is that of G and on the right hand side that of H. From this property, one can deduce that h maps the identity element eG of G to the identity element eH of H, and it also maps inverses to inverses in the sense that | |
I |
|---|
Identity matrixThe identity matrix is a square diagonal matrix with ones on the diagonal. | |
Image/ˈɪm.ɪdʒ/ Let f be a mapping of X to Y. Image of f is set {f(x):x fromX} and is denoted f(X). | |
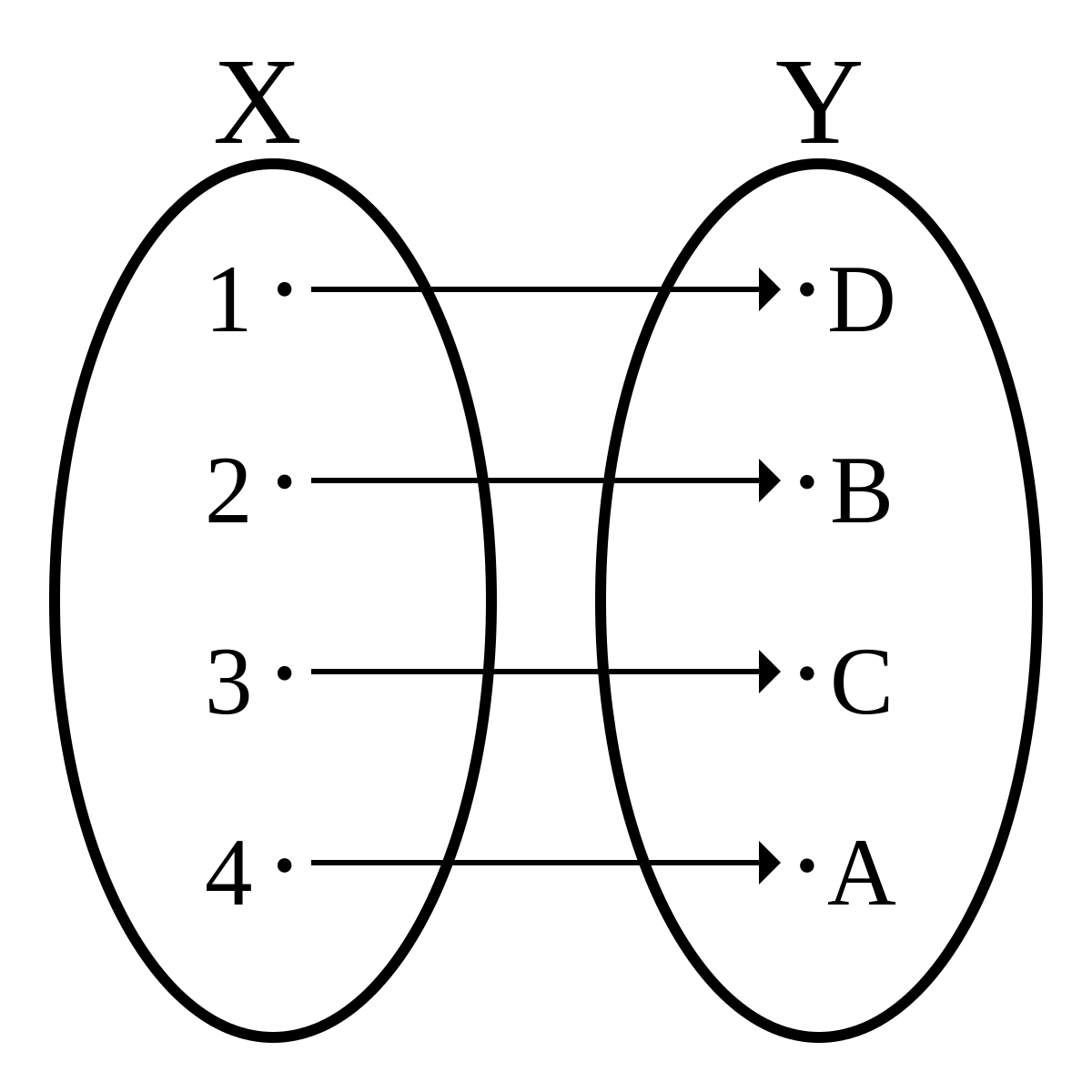
InjectionNoun
| |
Inner productnoun pronunciation: [ ˈɪnə ˈprɒdʌkt ] meaning: An inner product is a generalization of the dot product. In a vector space, it is a way to multiply vectors together, with the result of this multiplication being a scalar. More precisely, for a real vector space, an inner product 1. 2. 3. 4. example: For Euclidean space
| |
Integral domainnoun pronunciation: [ˈintigrəl dōˈmān] meaning: is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. example: The ring property: In an integral domain, every nonzero element a has the cancellation property, that is, if a ≠ 0, an equality ab = ac implies b = c. | |
invertibleadj. Etymology classical Latin invertere to turn upside down or inside out, to reverse, to turn over violently, upset, to turn round, to pervert, to reverse (an order), to cause words to convey the opposite sense (e.g. by irony), to change, alter, to paraphrase, to translate < in- in- prefix2 + vertere vert v.1 Pronunciation Meaning Of a function or other element of an algebraic structure: having an inverse for every a there exists b such that a*b^(-1)=1
https://www.oed.com/view/Entry/99024?rskey=IAlWbP&result=2&isAdvanced=false#eid | |
Irreducible (polynomial)Adjective Pronunciation
| |
K |
|---|
KernelNoun
The task is to solve
which can be computed by Gaussian elimination.
| |
L |
|---|
linear spanPronunciation: /ˈlɪniə(r) spæn/ Definition: Let be given a vector space V over a field K. The span of a set S of vectors is defined as the smallest subspace of V, which contains S. | |
M |
|---|
Matrix | |
MinorNoun Related terms Etymology | |
MonomialNoun, adjective Pronunciation | |
Moore-Penrose inverseFor A∈ℂ^(n x m), the Moore-Penrose inverse A^(+)∈ℂ^(m x n) is a matrix, satisfying all of the following conditions: The Moore-Penrose inverse exists for any A and is unique.
| |
N |
|---|
Normal subgroupLet G be a group and H a subset of G. H is called normal subgroup if it is a subgroup of G and for everey a element of G holds aH=Ha. Note: The property of being a subgroup is important, do not forget to validate if searching for normal subgroup. | |
P |
|---|
PermutationNoun Pronunciation The permutation means the action of rearrangement of the elements for another in a set. More formally: The permutation π in Sn is defined as a bijection from a set Sn onto itself. All permutations of a set with n elements create a symmetric group Sn, where the group operation is function composition. It holds four group axioms for two permutations π and σ in Sn: closure, identity, invertibility, and associativity. The composition of two permutations is not commutative.
The permutation stands for a number of combinations when the order does not matter following this formula:
Examples
Related terms Etymology | |
PivotNoun, (verb - see below)
| |
polynomialn. and adj. Pronunciation /ˌpɒlɪˈnəʊmɪəl/ Meaning Originally: an expression consisting of many terms, a multinomial. Now: spec. a sum of one or more terms each consisting of a constant multiplied by one or more variables raised to a positive (or non-negative) integral power (e.g. x4 − 3x2y + 7). Etymology Origin: Formed within English, by compounding. Etymons: poly-, -nomial OED | |
Prime (number)noun Pronunciation: Meaning: a positive integer greater than 1 which can be divided without a remainder only by numbers 1 and itself Source: https://www.oed.com/view/Entry/266923#eid71284393
| |
projectionnoun Pronunciation: /prəˈdʒekʃ(ə)n/ Definition: The linear operation, which two-times implicated gives the same result as identical operation is called projection. Sorce: | |
R |
|---|
RankNoun
| |
ringnoun Pronunciation: /rɪŋ/ Definition: Ring is an algebraic structure defined as 5-tuple of set, binary operations on this set (addition and multiplication), one unary operation (addition inverse) and one nullary operation (0). And the following axioms hold.
source: | |
Root (of a polynomial)noun Pronunciation: [ru:t] Meaning: a number z such that the value of the polynomial at z equals 0 Source: | |
S |
|---|
ScalarScalar, adj. and n. Pronounciation: /ˈskeɪlə/, /ˈskeɪlɑː/ Meaning: Noun: In quaternions, a real number. More widely, a quantity having magnitude but no direction, and representable by a single real number. Adjective: Of the nature of a scalar. Source:
| |
Singular matrixA singular matrix is a matrix which is not invertible. | |
Singular value | |
Singular value decompositionA singular value decomposition of a complex mxn matrix A is three matrices U, V, ∑, where U is an mxm complex unitary matrix, V is an nxn complex unitary matrix, and ∑ is an mxn diagonal matrix with non-negative real values on the diagonal, such that A=U∑V*.
| |
Subgroup/ˈsʌbˌɡruːp/ Let (G, *, ',e) be a group. Let H be a subset of G. We say, that H is a subgroup of G if e is element of H, and for every a,b elements of H are a*b and a' elements of H. For pronunciation: https://dictionary.cambridge.org/dictionary/english/subgroup | |
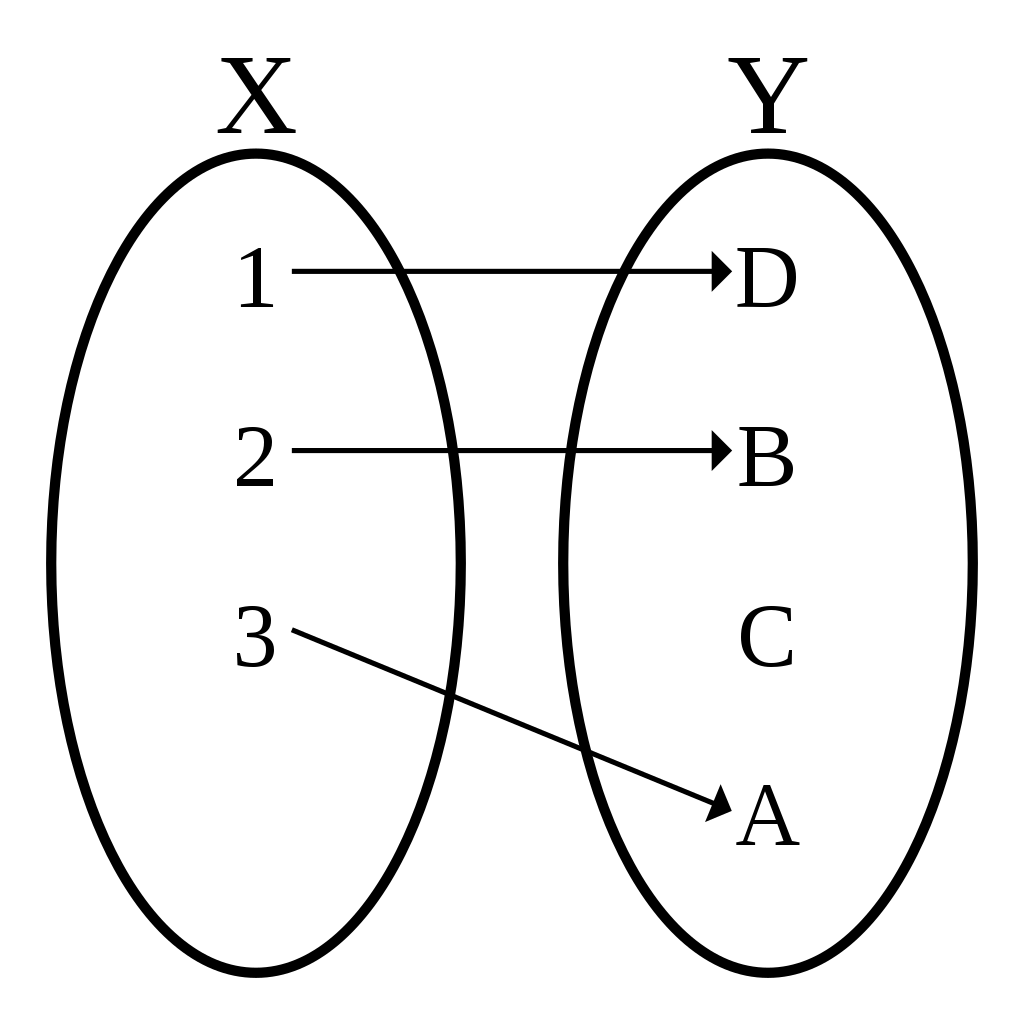
SurjectionNoun
| |
T |
|---|
Trace/treɪs/ Let A be a square matrix. The trace(A) is defined as sum of all elements on the main diagonal. | |
V |
|---|
VectorVector, n. Pronounciation: /ˈvɛktə/ Meaning: 1) An ordered set of two or more numbers (interpretable as the co-ordinates of a point); a matrix with one row or one column; also, any element of a vector space. 2) A quantity having direction as well as magnitude, denoted by a line drawn from its original to its final position. Source: | |
vector spacen. Pronunciation /ˈvɛktə speɪs/ Meaning a group whose elements can be combined with each other and with the elements of a scalar field in the way that vectors can, addition within the group being commutative and associative and multiplication by a scalar being distributive and associative. | |
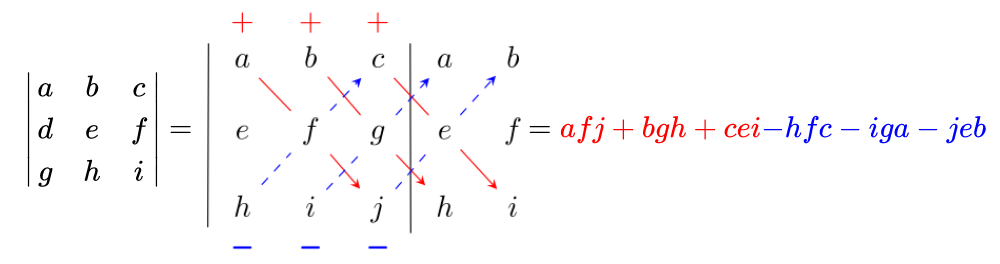








 .
.
![K[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bb4d802ca5718a14dc961af8692f35cdfad169b)




![{\displaystyle \mathbb {Z} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d4da3ac703cc7721ebba91a53f6752de7157124)

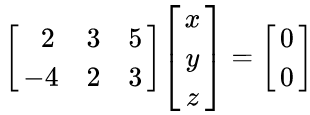 .
.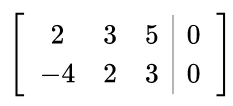 ,
,