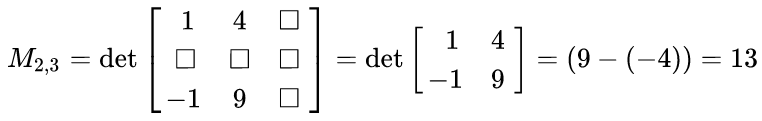Algebra - vocabulary

Procházet slovníkem pomocí tohoto rejstříku

Speciální | A | Á | B | C | Č | D | Ď | E | É | Ě | F | G | H | CH | I | Í | J | K | L | M | N | Ň | O | Ó | P | Q | R | Ř | S | Š | T | Ť | U | Ú | Ů | V | W | X | Y | Ý | Z | Ž | VŠE

Stránka: (Předchozí) 1 2 3 4 5 6 (Další)
VŠE

M

Matrix

Matrix, n.

Pronounciation:

Brit. /ˈmeɪtrɪks/

Plural:

matrices, Brit. /ˈmeɪtrᵻsiːz/

Meaning:

A supporting or enclosing structure.

Source:

OED

Minor

Noun

Pronunciation
/'mʌɪnə/ listen

Meaning
Minor of a matrixA is the determinant of a smaller square matrix. Minor M_ij is obtained from matrix A by removing the i-th row and the j-th column.

Example
Minor of the matrix

can be computed as

Synonym
Subdeterminant

Related terms
Minor expansion of a determinant

Etymology
Anglo-Norman and Old French, Middle French menor, menour, menur smaller, lesser, younger (c1100; also used as noun in plural denoting people under the age of majority (13th cent.))

Source
OED

Monomial

Noun, adjective
Prefix: mono-
Suffix: -al

Pronunciation
/mɒˈnəʊmɪəl/ listen

Meaning
A monomial is a polynomial which has only one term.

Example
5x³

Antonym
Polynomial

Etymology
The prefix mono- means single + -nomial (in binomial n.); after French monôme monome n. (1691)

Source
OED

Moore-Penrose inverse

For A∈ℂ^(n x m), the Moore-Penrose inverse A^(+)∈ℂ^(m x n) is a matrix, satisfying all of the following conditions:

${\text{1.}}\quad AA^{+}A$ $=\;A$

${\text{2.}}\quad A^{+}AA^{+}$ $=\;A^{+}$

${\text{3.}}\quad (AA^{+})^{*}$ $=\;AA^{+}$

${\text{4.}}\quad (A^{+}A)^{*}$ $=\;A^{+}A$

The Moore-Penrose inverse exists for any A and is unique.

source

N

Normal subgroup

/ˈnɔː.məl ˈsʌbˌɡruːp/

Let G be a group and H a subset of G. H is called normal subgroup if it is a subgroup of G and for everey a element of G holds aH=Ha.

Note: The property of being a subgroup is important, do not forget to validate if searching for normal subgroup.

P

Permutation

Noun
Suffix: -tion

Pronunciation
/ˌpɜːmjʊˈteɪʃən/ listen

Meaning
1) Algebra:

The permutation means the action of rearrangement of the elements for another in a set. More formally: The permutation π in S_n is defined as a bijection from a set S_n onto itself. All permutations of a set with n elements create a symmetric group S_n, where the group operation is function composition. It holds four group axioms for two permutations π and σ in S_n: closure, identity, invertibility, and associativity. The composition of two permutations is not commutative.

2) Combinatorics:

The permutation stands for a number of combinations when the order does not matter following this formula:

Examples

This notation means σ(1) = 2, σ(2) = 5, σ(3) = 4, σ(4) = 3, and σ(5) = 1

This figure depicts the graphical illustration of the notation.

Similar words
to permutate     /'pəːmjʊteɪt/         verb
permutability    /pəˌmjuːtə'bɪlɪti/    noun         condition of being permutable
permutable       /pər'mjutəbəl/ adjective    it is possible to permutate it
permutant         /pə'mjuːtənt/         noun           the result from permutation
permutated /'pəːmjʊteɪtɪd/      adjective    it has been subjected to permutation
permutating      /'pəːmjʊteɪtɪŋ/      adjective    undergoing permutation

Related terms
Even permutation
Odd permutation

Etymology
From French permutation, Latin permūtātiōn-, permūtātiō, Anglo-Norman permutacioun, Anglo-Norman and Middle French permutacion

Sources
OED
Figure

Pivot

Noun, (verb - see below)

Pronunciation
/'pɪvət/ listen

Synonym
Pivot element

Meaning
A pivot is an element on the left-hand side of a matrix for solving a system of linear equations using the Gaussian elimination that you want the elements above and below to be zero.

Example
The green 3 is a pivot. The aim is to make yellow numbers into zero.

Similar words
To pivot /'pɪvət/ verb to make an element above or below a leading one into a zero
Pivoting /'pɪvətɪŋ/ noun a process of making an element above or below a leading one into zero

Etymology
Middle French, French pivot, hinge (1338; 1174–78 in figurative use in the name of a dance), vertical main root of a fruit tree (1651), officer around whom troops wheel (1752)

Source:
OED

polynomial

n. and adj.

Pronunciation

/ˌpɒlɪˈnəʊmɪəl/

Meaning

Originally: an expression consisting of many terms, a multinomial. Now: spec. a sum of one or more terms each consisting of a constant multiplied by one or more variables raised to a positive (or non-negative) integral power (e.g. x4 − 3x2y + 7).

Etymology

Origin: Formed within English, by compounding. Etymons: poly-, -nomial

OED

Prime (number)

noun

Pronunciation:

[prʌɪm]

Meaning:

a positive integer greater than 1 which can be divided without a remainder only by numbers 1 and itself

Source:

https://www.oed.com/view/Entry/266923#eid71284393

projection

noun

Pronunciation:

/prəˈdʒekʃ(ə)n/

Definition:

The linear operation, which two-times implicated gives the same result as identical operation is called projection.

Sorce:

https://www.macmillandictionary.com

Stránka: (Předchozí) 1 2 3 4 5 6 (Další)
VŠE