Souhvězdí středové symetrie II

V minulé úloze se Megan snažila přesvědčit diváky, že hvězdy, na které ukazuje, tvoří středově symetrickou množinu. Poté, co někdo z publika namítl, že "ne, to teda netvoří", se teď Megan snaží situaci zachránit. Tvrdí, že množina hvězd možná není středově symetrická, ale že jde rozložit na dvě disjunktní množiny, které už obě samy o sobě středově symetrické jsou.

Formálně: máme množinu n bodů v rovině a chceme je obarvit černě a červeně tak, aby množina všech černých bodů byla středově symetrická a množina červených bodů taky. Pokud vám to pomůže, můžete předpokládat, že máte k dispozici řešení předchozí úlohy jako černou skříňku.

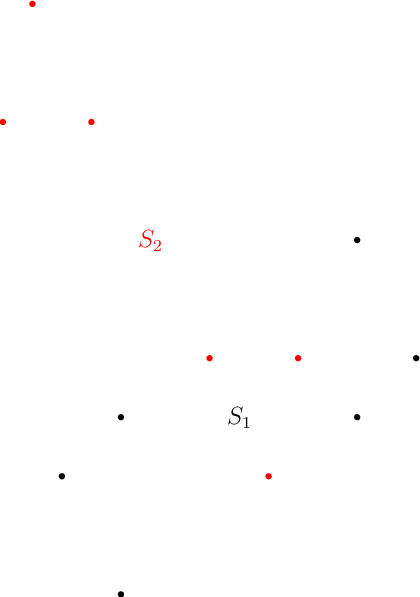
Příklad: Na následujícím obrázku je jedna možná množina bodů a její rozklad na dvě středově symetrické množiny. Všimněte si, že toto je jediné možné obarvení.