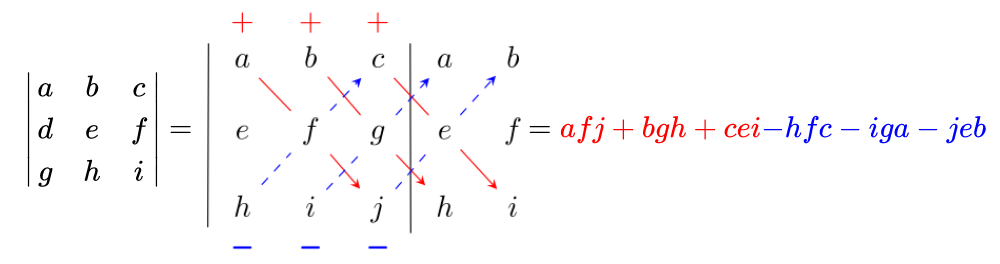Algebra - vocabulary

Noun

Pronunciation
/dɪˈtəːmɪnənt/ listen

Meaning
The determinant is a scalar value computed from the square matrix. It is denoted by det(A) or |A|, where A is a matrix. It is also used for determining the areas or volumes. For instance, the area of a parallelogram can be computed as the absolute value of the determinant of the matrix formed by the vectors representing the sides of the parallelogram.

Examples
The formula for the determinant of a 2 x 2 matrix:

Sarrus' scheme for the determinant of a 3 x 3 matrix:

Leibnitz formula for the determinant of an n x n matrix:


Etymology
Latin dētermināntem, present participle of dētermināre (to determine), French déterminant used in the paper Trevoux 1752

Sources
OED
Formulae: from WIKIPEDIA

Dimension, n.

Pronounciation:

/dɪˈmɛnʃən/

Meaning:

1) Geometry. A mode of linear measurement, magnitude, or extension, in a particular direction; usually as co-existing with similar measurements or extensions in other directions.

2) Algebra. Since the product of two, or of three, quantities, each denoting a length (i.e. a magnitude of one dimension), represents an area or a volume (i.e. a magnitude of two, or of three, dimensions), such products themselves are said to be of so many dimensions; and generally, the number of dimensions of a product is the number of the (unknown or variable) quantities contained in it as factors (known or constant quantities being reckoned of no dimensions); any power of a quantity being of the dimensions denoted by its index.

Source:

OED

noun

Pronunciation:

[dɪsˌtrɪbjʊˈtɪvɪti]

Meaning:

a property connecting addition and multiplication; for all numbers a, b, c it holds that a(b+c) = ac + bc and (a+b)c = ac + bc

Sources:

https://www.oed.com/view/Entry/55790?redirectedFrom=distributivity#eid

https://www.oed.com/view/Entry/55787#eid6517953

https://mathworld.wolfram.com/Distributive.html

noun

Pronunciation:

[dɒt 'prɒdʌkt]

Meaning:

the sum of the products of corresponding coordinates of two real vectors, or of the products of the coordinates of the second of two complex vectors and the complex conjugates of the corresponding coordinates of the first

Source:

https://www.oed.com/view/Entry/56962?redirectedFrom=dot+product#eid1265788880