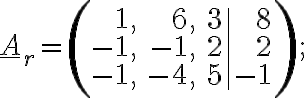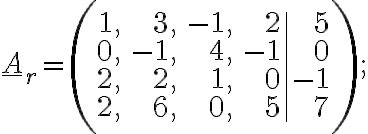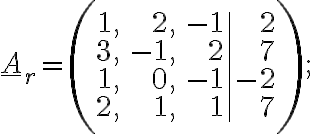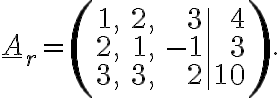Lineární rovnice – Příklady k procvičování
Требуемые условия завершения
1. Nalezněte všechna řešení soustavy rovnic v 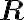 :
:
a) 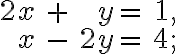
b) 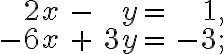
c) 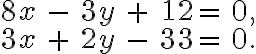
2. Užitím Frobeniovy věty rozhodněte, zda mají soustavy rovnic 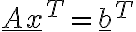 dané rozšířenou maticí
dané rozšířenou maticí
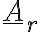 řešení v
řešení v 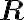 , jestliže
, jestliže
a)
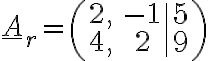
3. Řešte v 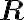 homogenní soustavy rovnic
homogenní soustavy rovnic 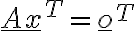 , jestliže
, jestliže
a) 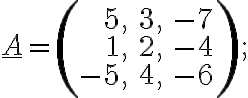
b) 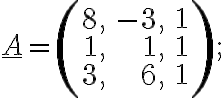
c) 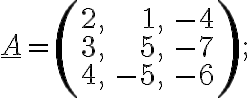
d) 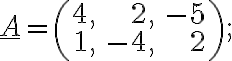
e) 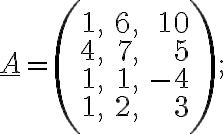
f) 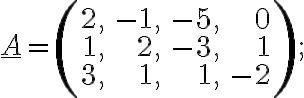
g) 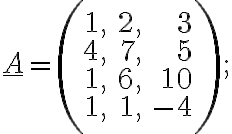
h) 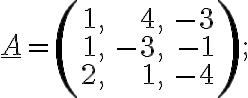
i) 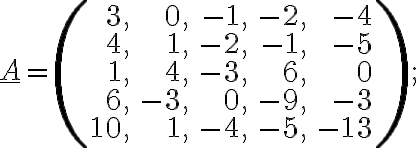
j) 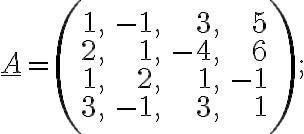
k) 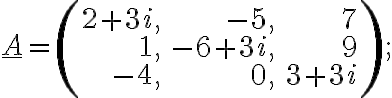
l) 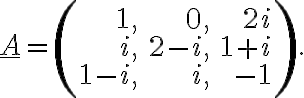
Řešení
1. a) 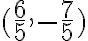 ; b)
; b) 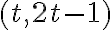 ,
, 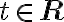 ; c)
; c) 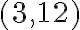 .
.
2. a) Ano; b) ano; c) ne; d) ano; e) ne.
3. a) 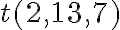
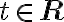 ; b)
; b) 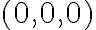 ; c)
; c) 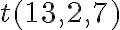
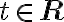 ; d)
; d) 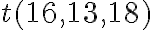
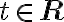 ; e)
; e) 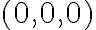 ; f)
; f) 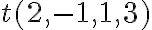
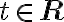 ; g)
; g) 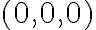 ; h)
; h) 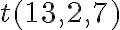
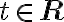 ; i)
; i) 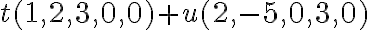
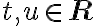 ; j)
; j) 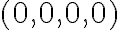 ; k)
; k) 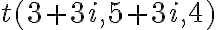
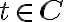 ; l)
; l) 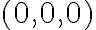 .
.
Последнее изменение: суббота, 3 августа 2013, 14:30